Итоги конкурса «Региональная Неделя Пифагора» 2021

О конкурсе проектов учащихся

Тема: «Сечения многогранников» непростая как в области теории, так и практики. Изучение данной темы на пропедевтическом уровне может оказаться весьма полезным. И, в основном, учащиеся 5-9 классов вместе со своими руководителями поняли правильно и создали адекватные продукты, уклоняясь от формулировок типа: «…секущая плоскость параллельна горизонтальной плоскости проекций.. ».

О конкурсах для учителей

Конкурс учителей математики по решению стереометрических задач координатно-векторным методом (КВМ), очевидно, состоялся. Во-первых, количество конкурсантов увеличилось по сравнению с предыдущими конкурсами профессионального мастерства. Во-вторых, была получена оценка степени рациональности применения данного метода к решению конкретных задач. Многие учителя указали на нерациональность использования КВМ при решении тех или иных пунктов приведенных в конкурсе задач. Некоторые привели, на их взгляд, наиболее рациональное геометрическое решение, а затем и решение с помощью КВМ.  Другие решили ограничиться только первым методом, проигнорировав требование конкурса: «Решить задачу координатно-векторным методом». Требования конкурса нужно выполнять или не участвовать вовсе.

В любом случае, вопрос о том, что легче, а что сложнее, носит субъективный характер. Мы не можем решить за ученика, что для него проще. Строить линейный угол двугранного угла и искать его косинус, синус или тангенс. Или же применить известный алгоритм решения данной задачи с помощью КВМ? Тоже самое можно сказать и о нахождении расстояния между скрещивающимися прямыми или о построении сечения (и прочее) с помощью КВМ. Да, может и проще построить сечение методом следов, но ведь КВМ дает нам координаты вершин многоугольника – искомого сечения призмы или пирамиды. А дальше, например, проверка параллельности его сторон или их равенства — задача примитивная. Конечно, можно и сочетать в решении оба метода. Мы должны научить решать правильно, открывая для учащихся новые пути решения задач и дать возможность ученику самостоятельно выбирать этот путь. «Категоричность» мнения, присущая многим учителям, проявляемая в неприятии других, «не таких как у него решений», думается, негативно влияет на развитие учащихся. Любое решение всегда можно проверить на правильность, указав на возможные иные более рациональные пути решения. В любом случае, данному методу уделяется недостаточное внимание, многие учащиеся его «боятся как огня». А этот метод хорошо «работает» и при решении планиметрических задач также в сочетании с геометрическим.

Подводя итоги конкурса рассмотрим некоторое замечания к работам конкурсантов.

1. Конкурс профессионального мастерства предполагает не только демонстрацию умения решать задачи правильно, при этом далеко не самые сложные, но и профессиональное представление самого решения. Одно дело читать работы с точки зрения профессионального человека, другое – с позиции ученика, которому должно быть понятно решение. Как построено сечение? (где этапы его построения?) Какая теорема лежит в основе данного этапа решения? (если факт не совсем очевидный для ученика) и пр. В некоторых работах следовало бы подробнее описывать шаги в решении задач.
2. Построение уравнения плоскости по трем точкам. Многие использовали понятие определителя. Научить раскладывать определитель по строке или применять правило Саррюса – задача не сложная. Но ведь это можно это сделать подстановкой координат точек в общее уравнение плоскости и это наиболее понятное действие для учеников. Если точка лежит в плоскости, значит, ее координаты удовлетворяют уравнению этой плоскости.
3. Если в четырёхугольнике две стороны лежат на параллельных прямых, это не означает, что он является трапецией. А где обоснование непараллельности двух других? Понятно, что очевидно, но складывается впечатление, что параллельность двух противоположных сторон – достаточное условие.
4. Если мы хотим доказать перпендикулярность векторов, достаточно найти их скалярное произведение. Зачем искать их длины и затем все это подставлять в формулу косинуса угла между рассматриваемыми векторами?
5. В условии задачи одни буквы, а на чертеже другие; брали конкретные значения длин ребер, которые отсутствовали в условии задачи и пр.

Некоторые проводили проверку принадлежности точки плоскости посредством подстановки её координат в найденное уравнение этой плоскости. Такое действие, безусловно, положительно влияет на дальнейшее решение, поскольку можно обнаружить ошибку сразу и «не тянуть» её далее.

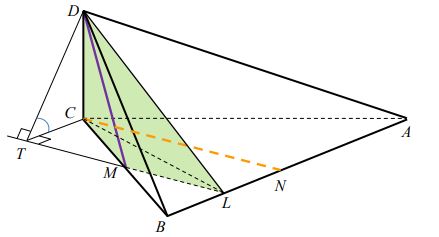
КВМ можно использовать и для построения сечений, конечно, в сочетании с известными теоремами, например, «секущая плоскость пересекает плоскости параллельных граней по параллельным прямым». Выделим фрагмент призовой работы (1 место), содержащей описание построения сечения по точкам, координаты которых найдены с помощью КВМ.

Обратите внимание на следующий интересный факт, который также можно использовать при решении задач КВМ, что и было предложено конкурсантами, занявшими призовые места (2 место).

При оценивании работ учитывались следующие критерии: правильность; реализуемость всех шагов в решении задач посредством КВМ (акцент на построение сечений: нахождение координат точки пересечения прямой и плоскости); наличие нескольких способов решения одной задачи с помощью КВМ; использование мало известных, но эффективных математических фактов.

Следует отметить, что конспекты открытых уроков (с точки зрения математики и методики обучения математике) стали более содержательными, однако их тематика, в большинстве случаев, не отвечает общей направленности конкурса.

С результатами конкурсов и работами можно ознакомиться по ссылке в облаке.

Всем спасибо за работу!!!!

← Вернуться к списку